Satuan Ukuran Sudut : Derajat

Secara umum, ada dua satuan yang digunakan dalam pengukuran sudut, yaitu derajat (°) dan radian (rad). Adapun hubungan antara keduanya adalah sebagai berikut :

1 r a d = 57, {2958...}^{\circ}

1^{\circ} = 0, 0174... r a d

Pertanyaannya adalah darimana angka-angka tersebut didapatkan. Untuk menjawab pertanyaan ini, kita dapat memulai dari definisi berikut.

Satu radian didefinisikan sebagai besar sudut pusat yang panjang busurnya sama dengan jari-jari.

Untuk menemukan hubungan radian dan derajat, kita dapat menggunakan konsep perbandingan sudut pusat dan panjang busur.

\frac{s u d u t p u s a t}{360^{\circ}} = \frac{p a n j a n g b u s u r}{k e l i l i n g}

sudut pusat = 1 rad
panjang busur = r
keliling = 2πr

Dengan menggunakan perbandingan diatas

\frac{1 r a d}{360^{\circ}} = \frac{r}{2 π r}

Jika disederhanakan akan diperoleh persamaan

π r a d = 180^{\circ}

Jika kedua ruas pada persamaan diatas dibagi π, akan diperoleh

1 r a d = \frac{180^{\circ}}{π} \approx 57, 29^{\circ}

dan jika kedua ruas dibagi 180, akan diperoleh

1^{\circ} = \frac{π}{180} r a d \approx 0, 02 r a d

Konversi Radian ke Derajat

Karena 1 rad =

\frac{180^{\circ}}{π}

, untuk mengubah x radian ke derajat dapat dilakukan dengan mengalikan x dengan

\frac{180^{\circ}}{π}

, ditulis

x r a d = x \cdot \frac{180^{\circ}}{π}

Contoh 1
Ubahlah sudut-sudut berikut dalam derajat
a.

\frac{π}{3}

rad = ... °
b. 4π rad = ... °

Jawab :
a.

\frac{π}{3}

rad =

\frac{π}{3}

\frac{180^{\circ}}{π}

= 60°
b. 4π rad = 4π .

\frac{180^{\circ}}{π}

= 720°

Konversi Derajat ke Radian

Karena 1° =

\frac{π}{180}

rad, untuk mengubah x derajat ke radian dapat dilakukan dengan mengalikan x dengan

\frac{π}{180}

rad, ditulis

x^{\circ} = x \cdot \frac{π}{180} r a d

Contoh 2

Ubahlah sudut-sudut berikut dalam radian

a. 30° = ... rad

b. 270° = ... rad

Jawab :
a. 30° = 30 .

\frac{π}{180}

rad =

\frac{π}{6}

rad
b. 270° = 270 .

\frac{π}{180}

rad =

\frac{3 π}{2}

rad

1. Ukuran Sudut dalam Derajat

Defenisi. Ukuran suatu sudut pusat untuk satu putaran penuh yaitu $360^{o}$ .

Dari definisi di atas dapat ditarik kesimpulan bahwa satu derajat ( $1^{o}$ ) merupakan besarnya sudut yang dibentuk oleh $\frac{1}{360}$ kali putaran.

2. Ukuran Sudut dalam Radian

Defenisi. Ukuran suatu sudut pusat yang besarnya sama yang panjang busurnya sama dengan jari-jari lingkaran.

Jika panjang busur tidak sama dengan r, maka cara menentukan besar sudut tersebut dalam satuan radian dapat dihitung dengan menggunakan perbandingan:

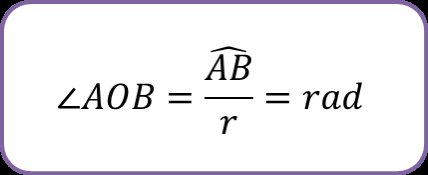
Sudut pusat suatu putaran penuh adalah 2π radian.

3. Hubungan antara Derajat dan Radian

Dari uraian di atas, maka dapat disimpulkan:

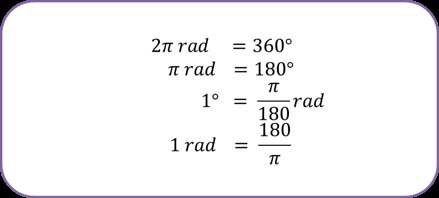
Contoh:

1. Nyatakan sudut-sudut berikut dalam ukuran radian!

$37^{o}$
$45^{o}$

Jawaban:

$37^{o} = 37^{o} \times \frac{\Pi }{180^{o}} rad = \frac{37}{180}\Pi rad$
$45^{o} = 45^{o} \times \frac{\Pi }{180^{o}} rad = \frac{45}{180}\Pi rad = \frac{\Pi }{4}rad$

2. Nyatakan sudut-suut berikut dalam ukuran radian!

$\frac{1}{3}\Pi \, \: rad$
$\frac{4}{5}\Pi \, \: rad$

Jawaban:

$\frac{1}{3}\Pi \, \: rad = \frac{1}{3}\Pi \times \frac{180^{o}}{\Pi } =60^{o}$
$\frac{4}{5}\Pi \, \: rad = \frac{4}{5}\Pi \times \frac{180^{o}}{\Pi } =144^{o}$

3. Nyatakan dalam bentuk derajat dan radian!

2 putaran
$\frac{3}{4}$ putaran

Jawaban:

$2\times 360^{o}=720^{o} \; atau \; 720^{o} = 720^{o}\times \left ( \frac{\Pi }{180^{o}} \right ) rad = 4\Pi \: rad$
$\frac{3}{4}\times 360^{o}=270^{o} \; atau \; 270^{o} = 270^{o}\times \left ( \frac{\Pi }{180^{o}} \right ) rad = \frac{3}{2}\Pi \: rad$

Catatan:

Sudut istimewa yang sering digunakan

Derajat	Radian	Derajat	Radian
$0^{o}$	$0\; rad$	$180^{o}$	$\pi\; rad$
$30^{o}$	$\frac{\Pi }{6}\; rad$	$210^{o}$	$\frac{7\Pi }{6}\; rad$
$45^{o}$	$\frac{\Pi }{4}\; rad$	$225^{o}$	$\frac{5\Pi }{4}\; rad$
$60^{o}$	$\frac{\Pi }{3}\; rad$	$240^{o}$	$\frac{4\Pi }{3}\; rad$
$90^{o}$	$\frac{\Pi }{2}\; rad$	$270^{o}$	$\frac{3\Pi }{2}\; rad$
$120^{o}$	$\frac{2\Pi }{3}\; rad$	$300^{o}$	$\frac{5\Pi }{3}\; rad$
$135^{o}$	$\frac{3\Pi }{4}\; rad$	$315^{o}$	$\frac{7\Pi }{4}\; rad$
$150^{o}$	$\frac{5\Pi }{6}\; rad$	$330^{o}$	$\frac{11\Pi }{6}\; rad$