MATEMATIKA WAJIB KELAS X MIA JUMAT 07 AGUSTUS 2020

ASSALAMUALAIKUM

MATERI MATEMATIKA SELANJUTNYA ADALAH

Sistem Persamaan Linear Tiga Variabel (SPLTV)

UNTUK ABSEN SILAHKAN PENCET DI SINI

Sistem Persamaan Linear Tiga Variabel- merupakan bentuk perluasan dari sistem persamaan linear dua variabel (SPLDV). Yang mana, pada sistem persamaan linear tiga variabel terdiri dari tiga persamaan yang masing-masing persamaan memiliki tiga variabel (misal x, y dan z).

Dengan begitu, bentuk umum dari Sistem Persamaan Linear Tiga Variabel dalam x, y, dan z dapat dituliskan seperti berikut ini:

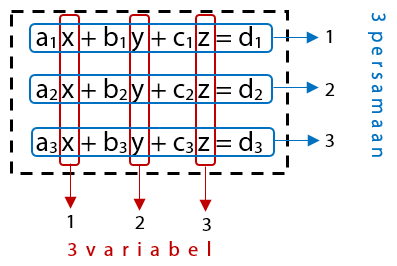
Sistem persamaan linear tiga variabel terdiri dari beberapa buah persamaan linear dengan tiga variabel. Bentuk umum dari persamaan linear tiga variabel adalah sebagai berikut.

ax + by + cz = d

a, b, c, dan d merupakan bilangan real, tapi a, b, dan c tidak boleh semuanya 0. Persamaan tersebut memiliki banyak solusi. Salah satu solusi dapat diperoleh dengan mengumpamakan sembarang nilai pada dua variabel untuk menentukan nilai variabel ketiga.

Sebuah nilai (x, y, z) merupakan himpunan penyelesaian sistem persamaan linear tiga variabel jika nilai (x, y, z) memenuhi ketiga persamaan yang ada di dalam SPLTV. Himpunan penyelesaian SPLTV dapat ditentukan dengan dua cara, yaitu metode substitusi dan metode eliminasi.

Metode Substitusi

Metode substitusi adalah metode penyelesaian sistem persamaan linear dengan cara menyubstitusikan nilai salah satu variabel dari satu persamaan ke persamaan lain. Metode ini dilakukan sampai diperoleh semua nilai variabel dalam sistem persamaan linear tiga variabel.

Metode substitusi lebih mudah digunakan pada SPLTV yang memuat persamaan berkoefisien 0 atau 1. Berikut adalah langkah-langkah penyelesaian dengan metode substitusi.

1. Tentukan persamaan yang memiliki bentuk sederhana. Persamaan dengan bentuk sederhana memiliki koefisien 1 atau 0.
2. Nyatakan salah satu variabel dalam bentuk dua variabel lain. Contohnya, variabel x dinyatakan dalam variabel y atau z.
3. Substitusikan nilai variabel yang diperoleh pada langkah kedua ke persamaan lain yang ada di SPLTV, sehingga diperoleh sistem persamaan linear dua variabel (SPLDV).
4. Tentukan penyelesaian SPLDV yang diperoleh pada langkah ketiga.
5. Tentukan nilai semua variabel yang belum diketahui.

Coba kita lakukan contoh soal berikut. Tentukan himpunan penyelesaian sistem persamaan linear tiga variabel di bawah ini.

x + y + z = -6 … (1)

x – 2y + z = 3 … (2)

-2x + y + z = 9 … (3)

Pertama, kita dapat mengubah persamaan (1) menjadi, z = -x – y – 6 menjadi persamaan (4). Kemudian, kita dapat menyubstitusikan persamaan (4) ke persamaan (2) sebagai berikut.

x – 2y + z = 3

x – 2y + (-x – y – 6) = 3

x – 2y – x – y – 6 = 3

-3y = 9

y = -3

Setelah itu, kita dapat menyubstitusikan persamaan (4) ke persamaan (3) sebagai berikut.

-2x + y + (-x – y – 6) = 9

-2x + y – x – y – 6 = 9

-3x = 15

x = -5

Kita sudah mendapatkan nilai x = -5 dan y = -3. Kita dapat memasukkannya ke persamaan (4) untuk memperoleh nilai z sebagai berikut.

z = -x – y – 6

z = -(-5) – (-3) – 6

z = 5 + 3 – 6

z = 2

Jadi, kita mendapat himpunan penyelesaian (x, y, z) = (-5, -3, 2)

SILAHKAN MATERI DI ATAS DI RANGKUM DAN DI PELAJARI

WASSALAM